Raymarching from Scratch (Part 2)

Rendering our first Sphere

Unshaded Sphere

We are ready to render our first sphere.

Lets start with defining the SDFs. In your shader create 2 new functions after uniform variables definitions:

... // uniforms

float sdSphere( vec3 p, vec3 c, float r )
{
    return length(c - p) - r;
}

float sdf(vec3 pos)
{
    return sdSphere(pos, vec3(0), 1);
}
...

sdf is our main function. It tells us how far the point pos is from the scene. sdSphere is a SDF for a sphere. We pass it our position p, centre of the sphere c and its radius r.

Lets implement the Raymarching algorithm:

... // sdf
vec3 raymarch(vec3 rayDir)
{
    vec3 hitColor = vec3(1.0, 1.0, 1.0);
    vec3 missColor = vec3(0.0, 0.0, 0.0);

    float depth = 0.0;
    for (int i=0; depth<MAX_DIST && i<MAX_STEPS; ++i)
    {
        vec3 pos = cameraPos + rayDir * depth;
        float dist = sdf(pos);
        if (dist < MIN_HIT_DIST) {
            return hitColor;
        }
        depth += dist;
    }
    return missColor;
}

As you can see, it is a very simple algorithm. We march along the ray at most MAX_STEPS times. We use ray equation

to compute current position in space. We use sdf to check if we have hit an object. If we have, we return return white color, otherwise march along the ray again. If we have not hit the ray in MAX_STEPS steps, we return black color.

Lets use this function in our main shader function:

void fragment()
{
    vec2 resolution = 1.0 / SCREEN_PIXEL_SIZE;
	
    vec3 rayDir = getRayDirection(resolution, UV);
    vec3 raymarchColor = raymarch(rayDir);
    COLOR = vec4(raymarchColor, 1.0);
}

And add these 3 uniforms at the top of the file:

uniform int MAX_STEPS = 250; // march at most 250 times
uniform float MAX_DIST = 20; // don't continue if depth if larger than 20
uniform float MIN_HIT_DIST = 0.00001; // hit depth threshold

Save the shader and run application. You should see white circle on a black background like here:

If you are stuck, you can use my project on GitHub. git checkout part2-unshaded will do the trick.

Phong Lightning Model

Basic Idea

All we can see now is a white circle on a black background. You might even think that our sphere isn’t spacial at all! And you are somewhat right – without the lights our scene looks flat. We need to implement a light model in order for the sphere to appear volumetric.

We will implement Phong light model. It states that the illumination of an objectconsists of the 3 parts

• Ambient component – no scene is completely black.
• Diffuse component – dirrect impact of the light.
• Specular component – glossiness of an object.

To gain better intuition, check out this link: LearnOpengl, Basic Lighting. On Wikipedia you can find formula we will be using in this tutorial:

Scary but in the end it all comes down to the 3 bullet points:

• Pixel color is deternined by the sum of the 2 components:
  • Ambient lightning, uniform for every object on the scene.
  • Sum of contributions of all light sources
• Each light source contribution is a sum of 2 parts:
  • The diffuse lightning – simulates the directional impact a light has on an object.
  • The specular lightning – simulates the bright spot of a light that appears on shiny objects.

In shader code:

vec3 ambientFactor = ambient * ambientCoeff;

vec3 sumOfLights = vec3(0);

for (int i=0; i<lightSourcesCount; ++i)
{
    vec3 diffuseFactor = ...;
    vec3 specularFactor = ...;
    sumOfLights += diffuseFactor + specularFactor;
}

return ambientFactor + sumOfLights;

Normal Vector and a Diffuse Lightning

Now, we have to discuss the normal vector of a surface. What is it and why should you bother? Well, normal to a surface at some point is a unit vector that is orthogonal to the surface at that specific point:

You need this vector in order to compute the diffuse lightning contribution. Lets say the a we have a toLight and a normal vectors. toLight is a unit vector from the hit point to the light source position:

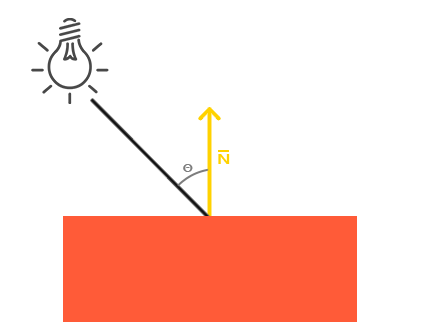
vec3 toLight = normalize(lightPosition - position);

Because toLight and normal are unit vectors, their dot product is equal to a cosine of an angle between the vectors:

The more toLight and normal are aligned in the same direction, the stronger light reflects from the surface. The contribution cannot be negative, so if cosine is negative we set the contibution to 0.

The final formula looks like this:

vec3 diffuseFactor = lightColor * max(0.0, dot(normal, toLight));

How do we compute the normal to a surface? Well, the normal vector is equal to a nomalized gradient of a SDF at given point. Gradient is a vector that tells us how fast the function grows in small change of its parameters. Feel free to read more about it here. All you need to know for now is that it can be approximated using nothing but SDF itself.

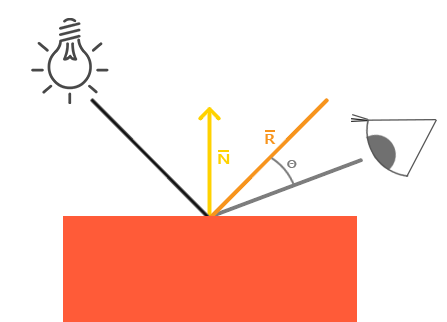
Specular Component

Finally, we want to compute the specular lightning contribution. It is computed by the following formula:

vec3 toEye = normalize(cameraPos - position);
vec3 toLight = normalize(lightPosition - position);
vec3 reflection = reflect(-toLight, normal);
float specularAngleCos = max(0.0, dot(toEye, reflection));
vec3 specularFactor = lightColor * pow(specularAngleCos, specularExponent)
                    * specularCoeff;

Putting it all together

Lets implement the Phong model in our shader! First of all lets define some uniform variables:

uniform float globalAmbient = 0.1; // how strong is the ambient lightning
uniform float globalDiffuse = 1.0; // how strong is the diffuse lightning
uniform float globalSpecular = 1.0; // how strong is the specular lightning
uniform float globalSpecularExponent = 64.0; // how focused is the shiny spot
uniform vec3 lightPos = vec3(-2.0, 5.0, 3.0); // position of the light source
uniform vec3 lightColor = vec3(0.9, 0.9, 0.68); // color of the light source
uniform vec3 ambientColor = vec3(1.0, 1.0, 1.0); // ambient color

We need to compute normal vector to the surface we have hit. Here is the function:

vec3 estimateNormal(vec3 p) {
    return normalize(vec3(
        sdf(vec3(p.x + DERIVATIVE_STEP, p.y, p.z)) - sdf(vec3(p.x - DERIVATIVE_STEP, p.y, p.z)),
        sdf(vec3(p.x, p.y + DERIVATIVE_STEP, p.z)) - sdf(vec3(p.x, p.y - DERIVATIVE_STEP, p.z)),
        sdf(vec3(p.x, p.y, p.z  + DERIVATIVE_STEP)) - sdf(vec3(p.x, p.y, p.z - DERIVATIVE_STEP))
    ));
}

We check how SDF changes when we change X, Y and Z coordinates by a small amount (arount 0.0001). For X, we compute SDF in points (X+0.0001, Y, Z) and (X00.0001, Y, Z) and subtract these values. We repeat this for Y and Z. Then we normalize the resulting vector.

We are ready to implement Phong model. Here is my function:

vec3 blinnPhong(vec3 position, // hit point
                vec3 lightPosition, // position of the light source
                vec3 ambientCol, // ambient color
                vec3 lightCol, // light source color
                float ambientCoeff, // scale ambient contribution
                float diffuseCoeff, // scale diffuse contribution
                float specularCoeff, // scale specular contribution
                float specularExponent // how focused should the shiny spot be
)
{
    vec3 normal = estimateNormal(position);
    vec3 toEye = normalize(cameraPos - position);
    vec3 toLight = normalize(lightPosition - position);
    vec3 reflection = reflect(-toLight, normal);
    
    vec3 ambientFactor = ambientCol * ambientCoeff;
    vec3 diffuseFactor = diffuseCoeff * lightCol * max(0.0, dot(normal, toLight));
    vec3 specularFactor = lightCol * pow(max(0.0, dot(toEye, reflection)), specularExponent)
                     * specularCoeff;
    
    return ambientFactor + diffuseFactor + specularFactor;
}

Then we modify our raymarch function to return computed illumination color instead of plain white:

/* before change
...
if (dist < MIN_HIT_DIST) {
    return hitColor;
}
...
/*

/* after change */
if (dist < MIN_HIT_DIST) {
    return blinnPhong(pos, lightPos, ambientColor, lightColor,
           globalAmbient, globalDiffuse, globalSpecular, globalSpecularExponent);
}

Thats all the changes! Save the shader and run an application. You should see the same picture:

If you struggle, please feel free to use my GitHub project. git checkout part2-shaded should get you here.

With some parameter tweaking you can get the following result:

That is it for now! There is a lot more to cover but that’s as far as I am willing to go right now. You can continue exploring Raymarching from the Jemie Wong’s excellent blog. Cheers!